Technical Paper Title: A Simple Agglomerative Method for Constructing Phylogenetic Trees
Authors: Meesala Suresh Kumar, 4th Sem MTech, IT
Guide: A Kiran Kumar, MTech, Asst.Professor, Department of IT
College: Aditya Institute of Technology and Management
The molecular mechanisms of widely studied organisms are astonishingly similar. This similarity Suggests that all organisms on Earth have a common ancestor. Essentially, this implies that any Randomly chosen set of species on Earth has is related to each other, however distantly. This relationship is called phylogeny, which is also the name of the branch in biology that studies the evolution of life forms.
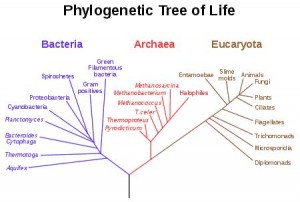
The relationship can be represented by a phylogenetic tree. The task of phylogenetics is to deduct this tree from observations upon existing organisms.
Earlier, the morphological characters have been used in constructing phylogenetic models. As we have now also molecular data available, we may use these data to derive the model. These data have shown surprisingly similar results compared to evolutionary trees constructer from morphological characters .
It is important to keep in mind, that not all of these data produces necessarily a correct output. When inferring a tree from a small subset of data, say, a single nucleotide, any deviation from standard “rate of change” or some unexpected mutation may lead to an (at least partially) incorrectly constructed tree. Trees inferred from the same set of species, but using different sequences, may well lead to a slightly different tree.
A taxon, sometimes called operational taxonomic unit or OTU, is an entity (such as species, aminoacid sequence, nucleotide sequence, language, etc.) Whose distance or similarity from other entities can be measured. The most interesting taxa from the point of view of computational biology are nucleotide and amino acid sequences.
A phylogenetic tree is a binary tree which describes the relation of several taxa (say, a certain nucleotide of a certain group of organisms). The binary form is mainly chosen to ease the calculations, which are very resource-consuming as such. The constructed tree has all the species in separate leaf nodes. Time goes from root to leaves. Some algorithms take the evolutionary rate into Consideration, and then relative times may be seen from the edges between any two nodes. In theory, it would then be possible to approximate the actual time if the evolutionary rate was known. The inner nodes above the leaf nodes and _represent the same species in the past. The common father of any two leaf nodes represents a point, where these two species diverged from a common Ancestral species. Some algorithms give also the root node, which represents the “ultimate ancestor”.
Fig: A phylogenetic tree showing relations of seven species.
Distance measuring
Phylogenetic tree construction uses distances between sequences when determining relations. When Constructing a phylogenetic tree based on data from protein or nucleotide sequence comparisons we first do a multiple alignment for the sequences and then calculate distance measure Dij between all taxa. Sequence alignment and distance measuring methods are often time-consuming and complicated.
Molecular clock
In assigning branch lengths to phylogenetic tree, one must consider whether evolutionary rate is constant. The determination of a phylogenetic tree for the evolution of species from amino acid or nucleotide sequence comparisons depends on measurements and assumptions concerning the rate of evolutionary change, i.e. a molecular clock. This is not a simple task when comparing homologous sites in two sequences, since over long periods of time, there can be back mutations
(The site in one sequence may originally contain A, later be mutated to G, then again to A) as well as parallel mutations (homologous sites in two sequences undergo the same mutation). Also the rate of evolution often varies over time and is significantly different for different species and different sequences.
Metric properties of distances
In order to be useful, a distance function must fulfill the definition of a metric. Metric is property that defines some basic behavior of the function in order for the distances to be sensible.
A metric properties must satisfy the following :
2. d(x ,y) = d (y , x) (symmetry).
3. d(x, z) ≤ d (x,y) + d (y,z) (triangle inequality).
Metric has some advanced properties as well. The most important ones from the viewpoint of the algorithms are additive metric and ultra metric.
Additive metric
If molecular clock property holds for a tree, it also satisfies the additive property. Additive metric simply states that distance between any pair of leaves i , j is the sum of the edge lengths along the path connecting them in the tree.
Assume that positive edge weights are assigned to a tree ‘I’. If the value of the distance function between all leaves i,j of ‘I’ is simply the sum of edge weights along the path connecting i and j (i.e. the path length between i, j), then d is called an additive tree metric.
UPGMA
Unweighted Pair Group Method with Arithmetic Mean (UPGMA) is a clustering method for building
phylogenetic trees. Clustering algorithms attempt to repeatedly cluster the data by grouping the closest elements. The result is a rooted tree with original sequences at the leaves. UPGMA constructs the tree correctly, if it satisfies the ultra metric property.
Initially, all the sequences are put to their own clusters. Each cluster is then assumed to be a leaf in the final tree. At each stage, we combine two clusters and simultaneously create a new node on the tree representing the new cluster.
Conclusion
UPGMA is not a widely used method anymore. It is rather old and very simple, and there exists nowadays many more efficient and trustworthy methods. However, this algorithm shows the principles on all clustering methods and serves as such a theoretical basis for others.
A major drawback in the algorithm is that it does not know how to handle non-ultra metric matrices. This has been corrected in many other algorithms thereafter.
Download the Complete Technical paper Here: Constructing Phylogenetic Trees