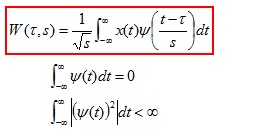Title: An Effective Approach for Color Image Transmission over OFDM for Video Broadcasting Applications
Authors: Vanga Sasi Devi & Mr. S V Naresh
Organisation: PNC & VIJAI Institute of Engineering & Technology, Repudi, Phirangipuram.
ABSTRACT
Image transmission over the fading channels without degrading the perceptual quality is a challenging task while mitigating the power consumption in many fields such as broadband networks, mobile communications, Image sharing and video broadcasting. Also, it is not possible to resend the lost packets every time in many applications such as video broadcasting. Here, an effective approach for color image transmission has been proposed with power saving approach over OFDM system. Experimental results shows that the reception quality of received image is good enough with various peak signal to noise ratios also saved 60% of energy.
Key words: Image transmission, OFDM, DWT, PSNR and video broadcasting
I. INTRODUCTION
In general, there is always a need for higher data rates over any communication network. But due to the inter symbol interference (ISI) and frequency selective fading channel such as Rayleigh fading channel, higher data rates will be limited [1], [2] and [3]. One of the best approaches to mitigate the ISI is multi-carrier modulation [4]. Orthogonal frequency division multiplexing is a well known multi-carrier modulation scheme that is having excellent performance which allows overlapping in frequency domain [5-6]. In OFDM, individual sub channels are affected by flat fading, so for a period of time, condition of the sub channels may be good, or they might be deeply faded. The packets which are transmitted through these faded sub channels are highly prone to be lost at the receiver due to non-acceptable errors [7]. OFDM system provides an opportunity to exploit the diversity in frequency domain by providing a number of subcarriers, which can work as multiple channels for applications having multiple bit streams. However, if some channel state information (CSI) (e.g., binary indication, like ‘good’ or ‘bad’) is available at the transmitter to know the packets are on the good or bad channels. The discrete wavelet transform (DWT) is used to compress the data packets that could be directly transmitted over the error-prone sub channels, with the coefficients having lower variances (i.e., with lower importance levels, high pass coefficients) mapped onto ‘bad’ sub channels. Thus, the more important coefficients are protected from likely losses in the transmission process. The lost coefficients in DWT image would still introduce lesser distortion. A key observation is that, the unequal importance level of the compressed image coefficients can be combined intelligently with the binary channel state feedback to achieve an improved transmission performance in delay-sensitive applications. This feedback can also be used further for energy saving in the transmission process with little or no trade-off in transmission performance.
In this paper, we explore the possibility of transmitting DWT images through the block fading OFDM channels with binary channel state feedback, where, unlike in conventional layered coded frame transmission, retransmission of lost packets are not allowed. Depending on the binary channel feedback and a predefined acceptable received power threshold, the ‘good’ and ‘bad’ (deeply faded) channels are sorted, and the coefficients in order of their importance levels are mapped to the sub channels belonging to the good ones. As an energy saving measure, if a coefficient is mapped onto a ‘bad’ sub channel, we propose that, it is discarded at the transmitter itself. Since our mapping scheme ensures that the discarded coefficients are of rather lesser importance, in most cases the transmitted frame could be reconstructed at the receiver with some distortion, without needing retransmissions. An application scenario of our proposed scheme could be real-time image/video transmission in peer-to-peer broadband communication systems. Prior work on DWT-OFDM system in studied the transmission of DWT compressed still frame over OFDM multipath channels. In that approach, the high pass coefficients were simply discarded before transmission. In contrast, in our approach, we consider the possibility of transmitting the low pass as well as high pass coefficients. We also explore the possibility of energy saving in transmission process over fading channel environment by discarding the coefficients of lower importance level through an informed decision process. Note that, as an alternative approach, adaptive modulation and coding (AMC) may prove to be a good solution for the OFDM system with full channel feedback. But it has a higher complexity in terms of optimization, and full channel feedback information is also less reliable in fast-changing environment due channel estimation error. On the contrary, under such fast fading channel conditions, the binary channel state information at the transmitter could be available more reliably and at a much lower overhead. This is because, in our approach, binary feedback corresponds to the comparison of the received signal strength with the threshold without resorting to any channel estimation technique.
In our proof of concept study, we generate four coefficients, after the first level DWT. Each coefficient in the form of a data vector is mapped on to a sub channel. We compare the energy saving and reception quality performance, by sending all coefficients over the mapped sub channels versus discarding the ones that are mapped on to the bad channels. Our results show that, up to 60% energy saving is possible at the low fading margins with a considerably high gain in the quality (PSNR) of the received image.
II. WAVELET ANALYSIS
The basic idea of this proposal is to use wavelets as a mean of extracting features from a voice signal. The wavelet technique is considered a relatively new technique in the field of signal processing compared to other methods or techniques currently employed in this field. Fourier Transform (FT) and Short Term Fourier Transform (STFT) [8] and [9] are the current methods used in the field of signal processing. However due to severe limitations imposed by both the Fourier Transform and Short Term Fourier Transform in analyzing signals deems them ineffective in analyzing complex and dynamic signals such as the voice signal [10] and [11]. In order to substitute the shortcomings imposed by both the common signal processing methods, the wavelet signal processing technique is used. The wavelet technique is used to extract the features in the voice signal by processing data at different scales. The wavelet technique manipulates the scales to give a higher correlation in detecting the various frequency components in the signal. These features are then further processed in order to construct the voice recognition system. Extracting the features of the voice signal does not limit the capabilities of this technique to a particular application alone, but it opens the door to a wide range of possibilities as different applications can benefit from the voice extracted features. Applications such as speech recognition system, speech to text translators, and voice based security system are some of the future systems that can be developed.
- Fourier Transform
The signal can be analyzed more effectively in frequency domain than the time domain, because the characteristics of a signal will be more in frequency domain. One possible way to convert or transform the signal from time to frequency domain is Fourier transform (FT). FT is an approach which breaks down the signal into different frequencies of sinusoids and it is defined as a mathematical approach for transforming the signal from time domain to frequency domain.
Fig.1. Analysis of FT with an example
FT has a drawback that it will work out for only stationary signals, which will not vary with the time period. Because, the FT applied for the entire signal but not segments of a signal, if we consider non-stationary signal the signal will vary with the time period, which could not be transformed by FT. and one more drawback that we have with the FT is we cannot say that at what time the particular event will has occurred.
- Short-Time Fourier Analysis
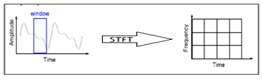
To correct the deficiency in FT, Dennis Gabor in 1946 introduced a new technique called windowing, which can be applied to the signal to analyze a small section of a signal. This adaptation has been called as the Short-Time Fourier Transform (STFT), in which the signal will be mapped into time and frequency information.
Fig.2. STFT analysis of a signal
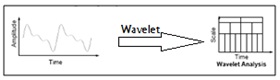
In STFT, the window is fixed. So, we this window will not change with the time period of the signal i.e., for both narrow resolution and wide resolution. And we cannot predict the frequency content at each time interval section. To overcome the drawbacks of STFT, a wavelet technique has been introduced with variable window size. Wavelet analysis allows the use of long time intervals where we want more precise low-frequency information, and shorter regions where we want high-frequency information.
Fig.3. Wavelet analysis with an example
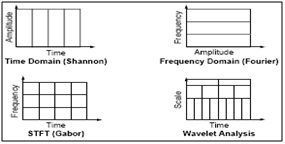
In fig.4 it is shown that the comparison of FT, STFT and wavelet transform by considering an example input signal and how the analysis of transformation techniques will apply to get the frequency information of input signal. We can observe that in wavelet analysis the graphical representation shows that the wavelet has more number of features than the FT and STFT. Wavelet is also called as multi resolution analysis (MRA). Here’s what this looks like in contrast with the time-based, frequency-based, and STFT views of a signal:
Fig.4. Comparison of FT, STFT and Wavelet analysis of a signal
- Discrete Wavelet Transform (DWT)
Discrete Wavelet Transform (DWT) is a revised version of Continuous Wavelet Transform(CWT). The DWT compensates for the huge amount of data generated by the CWT. The basic operation principles of DWT are similar to the CWT however the scales used by the wavelet and their positions are based upon powers of two. This is called the dyadic scales and positions as the term dyadic stands for the factor of two [12]. As in many real world applications, most of the important features of a signal lie in the low frequency section. For voice signals, the low frequency content is the section or the part of the signal that gives the signal its identity whereas the high frequency content can be considered as the part of the signal that gives nuance to the signal. This is similar to imparting flavor to the signal. For a voice signal, if the high frequency content is removed, the voice will sound different but the message can still be heard or conveyed. This is not true if the low frequency content of the signal is removed as what is being spoken cannot be heard except only for some random noise. The wavelet function is defined as follows:
The basic operation of the DWT is that the signal is passed through a series of high pass and low pass filter to obtain the high frequency and low frequency contents of the signal. The low frequency contents of the signal are called the approximations [13]. This means the approximations are obtained by using the high scale wavelets which corresponds to the low frequency. The high frequency components of the signal called the details are obtained by using the low scale wavelets which corresponds to the high frequency. From Figure 5, demonstrates the single level filtering using DWT. First the signal is fed into the wavelet filters. These wavelet filters comprises of both the high-pass and low-pass filter. Then, these filters will separate the high frequency content and low frequency content of the signal. However, with DWT the numbers of samples are reduced according to dyadic scale. This process is called the sub-sampling. Sub-sampling means reducing the samples by a given factor. Due to the disadvantages imposed by CWT which requires high processing power [14] the DWT is chosen due its simplicity and ease of operation in handling complex signals such as the voice signal. B. Wavelet Energy Whenever a signal is being decomposed using the wavelet decomposition method, there is a certain amount or percentage of energy being retained by both the approximation and the detail. This energy can be obtained from the wavelet bookkeeping vector and the wavelet decomposition vector. The energy calculated is a ratio as it compares the original signal and the decomposed signal.
Fig5. Demonstration of single level wavelet decomposition
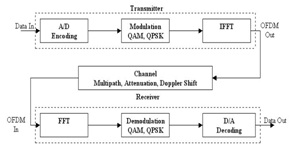
III. SYSTEM MODEL
In our system model, input color image is compressed using DWT, and the compressed data is arranged in data vectors, each with equal number of coefficients. These vectors are quantized and binary coded to get the bit steams, which are then packetized and intelligently mapped to the OFDM system, such that poorer sub channels can only affect the lesser important data vectors. We consider only one-bit channel state information available at the transmitter, informing only about the sub channels to be ‘good’ or ‘bad’. For a good sub channel, instantaneous received power should be greater than a threshold Pth. Otherwise, the sub channel is in fading state and considered ‘bad’ for that batch of coefficients. Note that the data transmitted through deeply faded sub channels are highly prone to error and are likely to be discarded at the receiver. Thus, the binary channel state information gives an opportunity to map the bit streams intelligently and to save a reasonable amount of power. Below, we described the DWTOFDM system model in details.
Fig.6 General OFDM block diagram
A. DWT-OFDM System
The proposed model is for transmission of DWT compressed data over OFDM channels in fading environment and illustrated in Fig. 7 and 8. The steps involved are as follows:
Step1: In the first step of proposed system initially we read the input image into the MATLAB
Step2: Then DWT is applied on a video frame of original size S1 ×S2 pixels, producing four sub-images: HL, LH, HH, and LL, each of the size pixels.
Step3: From these sub-images four coefficient vectors are generated, each of length .
Step4: The coefficient vectors are uniformly quantized and binary coded with L bits/coefficient to form four bit streams.
Step5: The bit streams are packetized and mapped on the OFDM system.
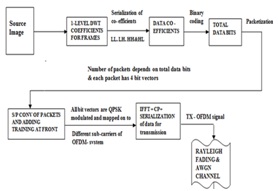
Fig7. Proposed Transmitter DWT-OFDM System
B. Packetizing and mapping onto the OFDM system
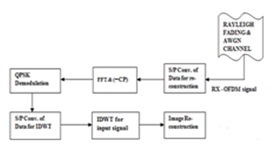
As described in Fig. 6, bit streams are packetized by chopping them into bit vectors of size NxN bits. Four such vectors are contained in a packet. Training bits are added at the front of each bit vector to estimate the SNR of the sub channels at the receiver. We illustrate the system by taking an example of OFDM system with IFFT size 128. Each bit vector in a packet is m-ary modulated, and 32 packets are simultaneously transmitted through different sub channels set. Here we use the feedback to decide the sub channel condition (‘good’ or ‘bad’), and accordingly re-arrange the data vectors to map them to the IFFT module. We propose a mapping scheme, which is proved to be efficient in terms of quality reception as well as energy savings. Packets are sent through frequency selective, slowly varying fading channel. The reverse process is done at the receiver with suitable treatments due to the discarded or lost data vectors.
Fig.8 Receiver section of Proposed DWT-OFDM system
C.Channel Model
In this study we use block fading channel model as in. The channel model is illustrated in Fig. 3, where M is the coherence bandwidth in terms of number of sub channels. In a block fading environment, M consecutive sub channels will simultaneously be either bad or good. Each such set consisting M sub channels is called a ’sub-band’. We denote total number of such sub-bands in the OFDM system as N. Thus, the total number of sub channels in the system is N × M. All sub-bands are independently faded with Rayleigh-distributed envelop, which corresponds to the block fading approximation in frequency domain. Our proposed mapping scheme generates a situation of subcarrier assignment for each data vector in a packet.
IV. FORMULATION
We now formulate the average distortion and energy savings in our proposed transmission scheme. We measure the system performance by probabilistic analysis of the average distortion in a block fading environment. In our interleaved coefficient mapping scheme, all the four sub channels per group of four coefficients are from different sub-bands. Thus, p will also be the probability of a sub channel to be bad. Let Pi = probability associated with the loss event i, for i= 0, 1, 2, 3, 4, which produces distortion Di.
Energy Saving Approach
In the proposed scheme the less important data vectors are discarded at the transmitter to save power if corresponding sub channel is in fading state. Denoting the percentage of data not transmitted in a packet as a measure of the percentage of energy saving, we can write energy saving expression as:
V. SIMULATION RESULTS
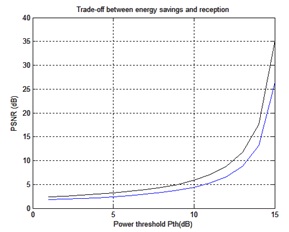
Simulation results have been done in MATLAB 2011a version and tested for various color images. The source image has been shown in fig8 (a), all the received output images after transmitting through the OFDM system using proposed scheme have been shown in fig9 (b), (c) and (d) with PSNR=21dB, 28dB and 38dB respectively. Trade off between power threshold and PSNR will be shown in fig10, in which the PSNR will be increased while increasing the power threshold value. Finally, 60% of the energy has been saved by the proposed algorithm by using the equation given in section IV.
Fig.9 (a) Source image, Output received images with different PSNR values after transmitting through OFDM channel (b) PSNR =21 dB (c) PSNR =28 dB and (d) PSNR=38 dB
VI.CONCLUSION
To conclude, we present a case of DWT compressed video transmission over OFDM channels where binary channel state information is available at the transmitter, but retransmission is not allowed. We propose a energy saving approach, where the compressed coefficients are arranged in descending order of priority and mapped over the channels starting with the good ones. The coefficients with lower importance level, which are likely mapped over the bad channels, are discarded at the transmitter to save power without significant loss of reception quality. Our analytic observations on reception quality and energy saving performance are validated by extensive MATLAB simulations.
Fig.10 Tradeoff between Pth and PSNR values
REFERENCES
- Gharavi and S. M. Alamouti, “Multi priority Video Transmission for Third Generation Wireless Communication Systems,” Proceedings of the IEEE, Vol. 87, No. 10, October 1999, pp1751-1763.
- G. Proakis, Digital Communications, McGraw-Hill, New York, 1989.
- Tarokh, N. Seshadri, and A. R. Calder bank, “Space-time codes for high data rate wireless communication: Performance criterion and code construction,” IEEE Tr. Information Theory 44, pp. 744–764, 1998.
- J. Cimini, “Analysis and simulation of a digital mobile channel using orthogonal frequency division multiplexing,” IEEE Trans. on Commun.COM-33, pp. 665–675, 1985.
- Kalet, “The multi tone channel,” IEEE Trans. on Commun. 37, pp. 119– 124, 1989.
- A. C. Bingham, “Multicarrier modulation for data transmission: an idea whose time has come,” IEEE Communication Magazine 28, pp. 5–14,1990
- Agrawal, V. Tarokh, A. Naguib, and N. Seshadri, “Space-time coded OFDM for high data-rate wireless communicatin over wideband channels,” Proc. VTC 98, pp. 2232–2236, 1998.
- Soontorn Oraintara, Ying-Jui Chen Et.al. IEEE Transactions on Signal Processing, IFFT, Vol. 50,No. 3, March 2002
- Kelly Wong, Journal of Undergraduate Research, The Role of the Fourier Transform in Time-Scale Modification, University of Florida, Vol 2, Issue 11 – August 2011
- Bao Liu, Sherman Riemenschneider, An Adaptive Time Frequency Representation and Its Fast Implementation, Department of Mathematics, West Virginia University
- Viswanath Ganapathy, Ranjeet K. Patro, Chandrasekhara Thejaswi, Manik Raina, Subhas K. Ghosh, Signal Separation using Time Frequency Representation, Honeywell Technology Solutions Laboratory
- Michael Unser, Thierry Blu, IEEE Transactions on Signal Processing, Wavelet Theory Demystified, Vol. 51,No. 2,Feb’13
- Valens, IEEE, A Really Friendly Guide to Wavelets, Vol.86, No. 11, Nov 2012,James M. Lewis, C. S Burrus, Approximate CWT with An Application To Noise Reduction, Rice University, Houston.
To download the above paper in PDF format Click on below Link: